重回帰分析とは | 簡単解説

重回帰分析の概要

アンケート調査の集計・分析では、質問項目や選択肢の関連性を定量的に評価したいというケースがあります。

ある業態の小売店舗の顧客満足度が、立地、価格、品揃え、接客といった要素のなかの何に最も影響されるかを分析する、あるいは、商品開発において、機能、性能、サイズ、デザインなどの各要素から、顧客の購入に結びつく可能性の高い価格水準を推定するといった場合です。

顧客満足度や価格は、店舗や商品に関わる複数の要因と因果関係があると考えられます。要因となるデータから結果となるデータを導き出す統計手法を「回帰分析」といいます。

要因となるデータを「説明変数」、結果となるデータを「目的変数」と呼び、説明変数がひとつである場合には「単回帰分析」、説明変数が複数ある場合は「重回帰分析」を用います。

多変量解析

複数の説明変数と目的変数の因果関係を明らかにする統計手法を総称して「多変量解析」といいます。重回帰分析は多変量解析の一手法であり、同様な手法に数量化1類があります。

重回帰分析と数量化1類の違いは、重回帰分析では数量データの説明変数と目的変数を扱うのに対し、数量化1類は説明変数として質的データを扱います。

質的データとは、性別や職業など名義尺度として表されるデータと、優先順位や好みの度合いといった順序尺度で表されるデータを指します。

重回帰分析で変数として扱えるのは量的データですが、質的データをダミー変数として量的データに置き換えることで、変数に質的データが含まれる場合でも重回帰分析を行うことが可能です。

重回帰分析の用途

重回帰分析はマーケティング以外にもさまざまな分野で活用されています。重回帰分析をデータ分析に用いる目的は、説明変数が変化した場合に目的変数がどう変わるかという「予測」を行う場合と、目的変数に対する各説明変数の「影響度」を評価する場合の2つが挙げられます。

売上予測

店舗の売上予測に重回帰分析が用いられます。チェーン店で新規出店を図る場合に、既存店舗の商圏人口、駅からの距離、店舗面積、席数、客単価、メニュー数などを説明変数とし、売上や来店客数を目的変数として重回帰分析を行います。

それぞれの説明変数の目的変数に対する影響度を数値化し、既存店舗の説明変数としたデータを新店舗に当てはめることで、新店舗の売上や来店客数を予測することができます。

人事管理

説明変数として業務量や残業時間などの数量データに加え、業務への満足度、上司や同僚との関係を点数化し、離職率を目的変数とした重回帰分析を行うことで、離職率を下げるための効率的なアプローチを検討することができます。

人事領域では営業マンの行動管理、昇進を決定する場合のパフォーマンス予測といった分野にも重回帰分析が用いられます。

その他の利用方法

• 農業分野で気温や降水量などの気象要因を説明変数とした病害虫の発生予測
• 企業のKPIを説明変数としPBR（株価純資産倍率）への貢献度の数値化
• 工場の生産ラインで設備の稼働状況やセンサーからの検出数値を説明変数として不良品の発生を予測
• SNSのインプレッション数、いいねの数、リツイート数を説明変数とし、SNS経由での訪問数を予測

エクセルを用いた重回帰分析の例

クロス・マーケティングのホームページで紹介している重回帰分析の具体例をもとに、エクセルを用いた重解分析の手順を紹介します。

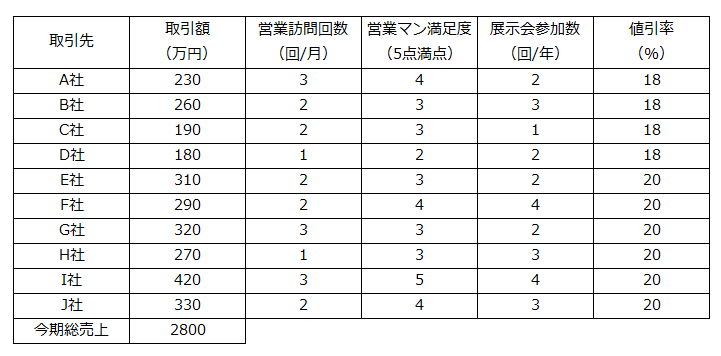
取引先別の営業データと取引実績から、次期の売上と売上に影響する要因を分析するケースを例に挙げてみましょう。営業データとして次の4つの要素を説明変数とし、取引先別の売上を目的変数とします。

【目的変数】

• 取引額：万円 / 年間

【説明変数】

• 営業訪問回数：回 / 月
• 営業マン満足度：得点 / 5点満点（非常に不満1点～非常に満足5点）
• 展示会参加回数：回 / 年（4半期ごとに1回開催される展示会への参加回数）
• 値引率：%

【営業データ】

エクセルの操作

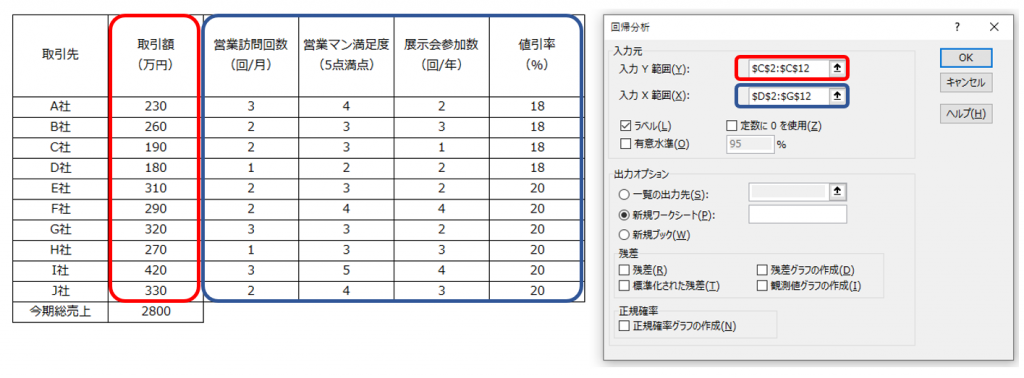
エクセルのアドオンから「データ分析」を追加し、「データ」タブから「データ分析」を選択します。データ分析から「回帰分析」を選択し、表示されたダイアログで以下を設定します。

目的変数とする「取引額」を「入力Y範囲」、説明変数とする「営業訪問回数」「営業マン満足度」「展示会参加回数」「値引率」の列全体を「入力X範囲」に指定し「OK」をクリックすると以下の結果が出力されます。

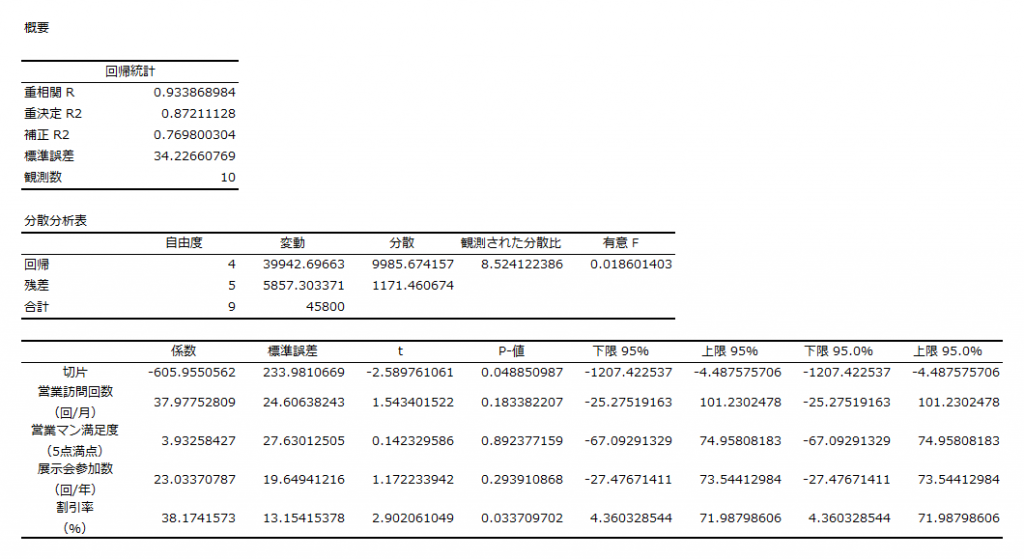
重回帰分析を行った結果が信頼できるものかどうかの判定を行います。

実績値である取引額と各説明変数の相関関係があるかどうかを判断するのが「重相関R」と「重決定R2」です。重決定R2は重相関係数を2乗したものであり、どちらも1に近いほど分析精度が高いと判断できます。

得られた回帰式の有意性を判断するのが分散分析表の「有意F」です0.05未満であれば回帰式が妥当であることを確認できます。

各説明変数の有意性について判断する指標が「t」と「P-値」です。t が 2 を超えている場合は目的変数に影響していると考えられ、P-値は0.05未満であれば説明変数と目的変数の関連性が高いと判断します。

回帰式を求め来期のシミュレーションを行う

出力結果から回帰式を求めます。出力結果の「係数」が回帰係数となります。

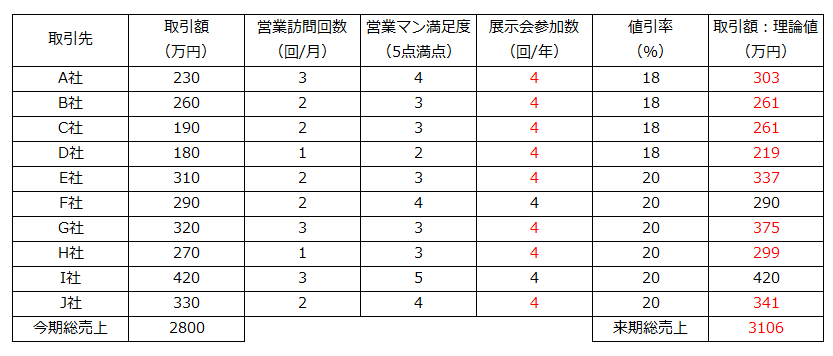
来季は年4回ある展示会にすべて参加するとした場合に、来季の会社別取引額がどれぐらい変化するかを回帰式を使って求めます。

【営業データシミュレーション】

来期の営業施策として展示会への参加回数を増やすことを想定した場合、全体の売上が306万円ほどアップするというシミュレーションが得られました。

③各説明変数の「寄与率」を求める

エクセルで求めた回帰係数は、「営業訪問回数」であれば、訪問回数を1回増やすと37.98万円分の売上増加が見込まれることを意味しています。

しかし、各説明変数の単位が異なるため、各回帰係数の数値を取引額に影響する度合いとして比較することはできません。

各説明変数の重要度を比較するためには、「営業データ」の単位の違いを取り除くための標準化という作業が必要です。標準化は以下の式を用いて行います。

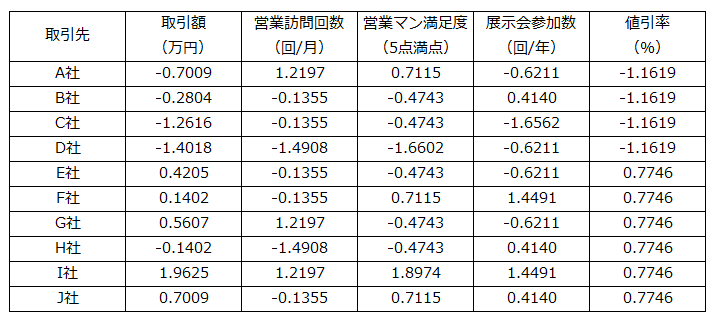
営業データの標準化を行うと以下の基準値が得られます。

【営業データ（基準値）】

営業データの実測値で求めたのと同様、上記の基準値をもとにエクセルで重回帰分析を行うと、以下の標準化回帰係数が得られます。

【要因の重要度】

	回帰係数	標準回帰係数	寄与率
営業訪問回数	37.9776	0.3928	30.1%
営業マン満足度	3.9326	0.0465	3.6%
展示会参加回数	23.0337	0.3119	23.9%
値引率	38.1742	0.5527	42.4%
合計		1.3039	100.0%

標準回帰係数は同列で比較することが可能であるため、標準回帰係数の合計を100%とした場合の各説明変数の標準回帰係数の割合が「寄与率」として算出されます。

寄与率を見ると、取引額に影響する重要度は、「値引率」が最も高く、「営業マン満足度」が最も低いということがわかります。

重回帰分析を行う場合の注意点

重回帰分析の結果だけをもって説明変数と目的変数の因果関係を保証できるものではないことに注意が必要で、以下の点を頭に入れておく必要があります。

• 説明変数と目的変数の構造が多層的で複雑な関係にある場合、分析精度が下がり解釈しづらいものになる。
• 分析で得られた因果関係が見せかけの相関であることもあり得る。
• 説明変数同士の関連性が高い場合、分析結果が偏りのあるものになる。（多重共線性）
• データの精度が低い場合、データ取得時に時間差がある場合など、正確な分析ができない。

まとめ

要因の分析や予測をデータとして提示できることはビジネスの現場で高い説得力をもつと同時に、適切な分析によって結果に結びつく意思決定を行うことが可能になります。

営業データの事例で示したように、ある程度まとまったデータがあれば比較的簡単に重回帰分析を行うことができることから、積極的に活用してみることをおすすめします。