AHP（階層分析法）とは｜簡単解説

2024年1月25日 2026年5月26日

AHP（階層分析法）のカンタン解説

AHP（階層分析法）は、問題解決に関わる要素を構造化し、各要素の重み付けから導かれる客観的評価を指標化して意思決定を行うための手法です。問題の構造を明確にできる点と、一対比較法を用いることで主観的な判断を統計的な数値に置き換える点が特徴です。

この記事でわかること

AHPとは、複数の評価基準と代替案を階層構造化し、一対比較で優先順位を算出する意思決定手法
重み付き評価法との違い
アンケート調査でのAHPの活用場面と具体例
AHP（階層分析法）とは

無料トライアルはこちら

AHP（階層分析法）とは

AHPはAnalytic Hierarchy Processの略で、階層分析法、階層化意思決定法とも呼ばれます。

AHPは、問題解決のための数学的な手法を研究するオペレーションズ・リサーチの分野から提案され、政府部門や軍事領域、産業分野などで広く用いられる意思決定のための手法です。

意思決定の全体像を、目的・評価基準・代替案の階層構造であらわし、人間の主観的判断を一対比較法によって重み付けした結果から合理的な判断を行うものです。

AHPの手順

AHPは、意思決定の構造を階層分けし、階層に含まれる要素を一対比較法による評価結果により重み付けを行います。

階層図の作成

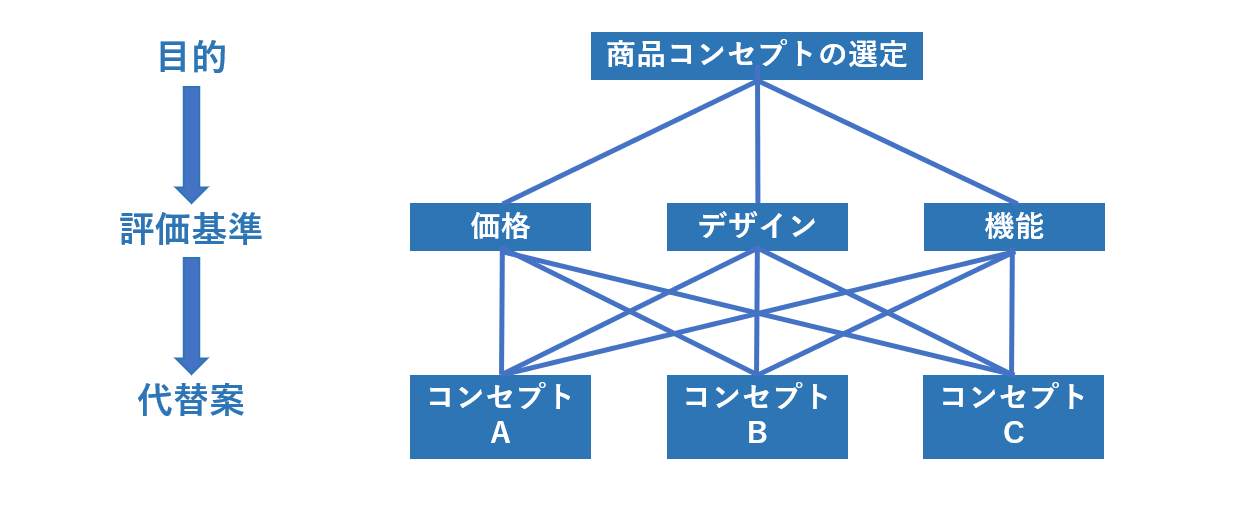
AHPで最初に行うのは、意思決定の構造全体を「目的」「評価基準」「代替案」の3つの階層構造に分けて整理する階層図を作成することです。

「目的」は意思決定の最終目的、「代替案」は与えられている選択肢、「評価基準」は代替案の選択に関わる基準を意味しています。

以下の例は、新商品のコンセプト開発にあたり、3つのコンセプト案のなかから1つに絞り込むためにAHPを用いるケースです。

このケースでは、目的を「商品コンセプトの選定」、評価基準を「価格・デザイン・機能」、代替案を「コンセプトA～C」と仮定します。

【階層図の例】

一対比較の実施

階層図の流れに沿って、最終目的からみた評価基準の優先順位付けを行い、評価基準からみた代替案の重要度を評価します。

評価基準の重み付けと評価基準による代替案の評価は一対比較法で行います。一対比較法は複数の選択肢から2つずつの組み合わせを提示し、1つの評価基準をもとに一方を選択、または、段階的な評価を求めるものです。

例に挙げた商品コンセプトの選定では、評価基準と各評価基準に照らした代替案、それぞれの一対比較を行うためのアンケートを実施します。

評価基準の一対比較

一対比較で評価するための組み合わせの数は評価基準の数に依存します。評価基準は価格・デザイン・機能の3つであるため、総当りの組み合わせは3通りです。

以下のマトリクスは価格・デザイン・機能の3つの評価基準を一対比較で評価する場合の質問票です。

評価基準を両極に配置するマトリクス形式の回答を用意し、3通りの組み合わせについて左右対称とする9段階の選択肢を設定します。

【評価基準の一対比較】

	絶対的に重要	かなり重要	重要	やや重要	同じ	やや重要	重要	絶対的に重要
価格	○	●	○	○	○	○	○	○	デザイン
デザイン	○	○	○	○	○	○	●	○	機能
機能	○	○	○	○	○	●	○	○	価格

代替案の一対比較

代替案の数は3つなので総当たりの組み合わせも3通りです。それぞれについて、価格・デザイン・機能の評価基準ごとに一対比較を行います。

【代替案の一対比較（価格）】

	絶対的に良い	かなり良い	良い	やや良い	同じ	やや良い	良い	かなり良い	絶対的に良い
コンセプトA	○	○	●	○	○	○	○	○	○	コンセプトB
コンセプトB	○	○	●	○	○	○	○	○	○	コンセプトC
コンセプトC	○	○	○	○	○	○	○	●	○	コンセプトA

【代替案の一対比較（デザイン）】

	絶対的に良い	かなり良い	良い	やや良い	同じ	やや良い	良い	かなり良い	絶対的に良い
コンセプトA	○	○	○	●	○	○	○	○	○	コンセプトB
コンセプトB	○	○	○	○	●	○	○	○	○	コンセプトC
コンセプトC	○	○	○	○	○	●	○	○	○	コンセプトA

【代替案の一対比較（機能）】

	絶対的に良い	かなり良い	良い	やや良い	同じ	やや良い	良い	かなり良い	絶対的に良い
コンセプトA	○	○	○	●	○	○	○	○	○	コンセプトB
コンセプトB	○	●	○	○	○	○	○	○	○	コンセプトC
コンセプトC	○	○	○	○	○	○	○	●	○	コンセプトA

一対比較表の作成とウェイト（重要度）の計算

上記の回答の集計結果から、それぞれの一対比較表の評定尺度を決定します。決定した尺度に対し、左側と右側でとな対照的な位置にある項目には、以下のように逆数のスコアを与えます。

	絶対的に重要	かなり重要	重要	やや重要	同じ	やや重要	重要	かなり重要	絶対的に重要
左側が基準の場合	9	7	5	3	1	1/3	1/5	1/7	1/9	右側の項目
左側の項目	1/9	1/7	1/5	1/3	1	3	5	7	9	右側が基準の場合

以下の場合、価格とデザインの比較では価格に近い「かなり重要」がマークされています。デザインに対して価格を基準とする場合は7となりますが、価格に対してデザインを基準とする場合は1/7ということになります。

【評価基準の一対比較】

	絶対的に重要	かなり重要	重要	やや重要	同じ	やや重要	重要	かなり重要	絶対的に重要
価格	○	●	○	○	○	○	○	○	○	デザイン
デザイン	○	○	○	○	○	○	●	○	○	機能
機能	○	○	○	○	○	●	○	○	○	価格

これらをもとに、評価基準の一対比較表と評価基準ごとの代替案の一対比較表を作成し、それぞれの評価基準の幾何平均を計算しウェイトを求めます。

【評価基準のウェイト】

	価格	デザイン	機能	幾何平均	ウェイト
価格	1	7	3	31×7×3＝2.579	2.579 / 4.121＝0.669
デザイン	1/7	1	1/3	317×1×13＝0.362	0.362 / 4.121＝0.088
機能	1/3	3	1	313×3×1＝1.000	1 / 4.121＝0.243
			合計	4.121	1.000

評価基準のウェイトと同様に代替案についても幾何平均からウェイトを計算します。

【代替案のウェイト（価格）】

	コンセプトA	コンセプトB	コンセプトC	幾何平均	ウェイト
コンセプトA	1	5	7	31×5×7＝3.271	3.271 / 4.577＝0.715
コンセプトB	1/5	1	5	315×1×5＝1.000	1.000 / 4.577＝0.218
コンセプトC	1/7	1/5	1	317×15×1＝0.306	0.306 / 4.577＝0.067
			合計	4.577	1.000

【代替案のウェイト（デザイン）】

	コンセプトA	コンセプトB	コンセプトC	幾何平均	ウェイト
コンセプトB	1/3	1	1	313×1×1＝0.693	0.693 / 3.467＝0.200
コンセプトC	1/3	1	1	313×1×1＝0.693	0.693 / 3.467＝0.200
			合計	3.467	1.000

【代替案のウェイト（機能）】

	コンセプトA	コンセプトB	コンセプトC	幾何平均	ウェイト
	コンセプトA	コンセプトB	コンセプトC	幾何平均	ウェイト
コンセプトB	1/3	1	7	313×1×7＝1.326	1.326 / 4.359＝0.304
コンセプトC	1/7	1/7	1	317×17×1＝0.273	0.273 / 4.359＝0.063
			合計	4.359	1.000

ここまでで求めたウェイトをまとめて以下の集計表を作成します。

【集計表】

評価基準	価格	デザイン	機能
評価基準のウェイト	0.669	0.088	0.243
コンセプトA	0.715	0.600	0.633
コンセプトB	0.218	0.200	0.304
コンセプトC	0.067	0.200	0.063

さらに、評価基準のウェイトと各代替案のウェイトにかけあわせた結果を合計して総合評価を求めます。

【総合評価】

評価基準	価格	デザイン	機能	総合評価値
コンセプトA	0.669×0.715＝0.478	0.088×0.600＝0.053	0.243×0.633＝0.154	0.685
コンセプトB	0.669×0.218＝0.146	0.088×0.200＝0.018	0.243×0.304＝0.074	0.238
コンセプトC	0.669×0.067＝0.045	0.088×0.200＝0.018	0.243×0.063＝0.015	0.078

事例では、ウェイトを算出するために幾何平均を使いましたが、これ以外に固有値法や対数最小二乗法といった、他の計算手法が用いられることもあります。

まとめ

AHPはマーケティング分野はもとより、紛争解決や軍事問題、政策決定や環境問題の解決など、幅広い分野で用いられる意思決定手法であり、それぞれの分野で数多くの実践と研究が行われています。

一対比較法を行う際に、評価基準と代替案の数が多い場合は評価に負荷がかかりますが、ウェイトの計算自体はわかりやすいことから、手順と考え方がわかれば幅広い分野に適用できます。

AHP（階層分析法）のFAQ

AHPと重み付き評価法の違いは何ですか？

AHPは複数の評価基準と代替案を階層構造化し、一対比較で優先順位を算出する意思決定手法を指します。一方、重み付き評価法はAHPとは異なる目的・場面で使われます。調査目的に応じた使い分けが重要です。

AHPはExcelで計算できますか？

AHPはExcelの関数・データ分析アドイン（「データ」タブ→「データ分析」）を活用して計算できます。基本的な手順は①データ整備②関数または分析ツール選択③結果の読み取りです。より高度な分析にはR・Python・SPSSの利用を推奨します。

アンケート調査でAHPはどのような場面で使いますか？

AHPはアンケートデータの集計・分析フェーズで活用されます。属性別のスコア比較、顧客セグメント分析、満足度要因の特定など、データから意味を引き出す際に使います。QiQUMOで収集したアンケートデータにそのまま適用できます。