確率分布とは｜簡単解説

確率分布とは

確率分布とは、確率変数がとり得る値と、それぞれの値が発生する確率を関数であらわしたものです。

事象

ランダムに起こる現象において、観測される可能性のある出来事や状態のことを事象といいます。

サイコロを振った時の1〜6までの出る目、コイントスを行った場合の裏表が事象です。実際にサイコロを振って出た1〜6までのどれか1つの目、コイントスを行って出た表、または、裏を実現値といいます。

確率

確率は、特定の事象が起こる可能性を数値で表したもので、0から1の間の割合で表します。確率をP、事象をX、実現値をxとし、事象Xが起こる確率をP(X＝x)とあらわします。この時の「X」を確率変数といいます。

離散型確率分布と連続型確率分布

確率変数は、サイコロの目やコインの裏表など、カテゴリや自然数、整数で表される離散型確率変数と、長さ、時間、温度など値と値の間にとり得る値が無限にある連続型確率変数に分けられます。

離散型確率変数に対応する確率分布が離散型確率分布、連続型確率変数に対応する確率分布が連続型確率分布です。

確率質量関数と確率密度関数

離散型確率分布を定義する関数を確率質量関数、連続型確率分布を定義する関数を確率密度関数といいます。

確率質量関数をグラフで表した場合の確率は縦軸に相当します。確率密度関数の場合は横軸と曲線で囲まれた部分の面積が確率に相当します。

確率分布の期待値と分散

確率分布の期待値は、実現値と確率の積の総和で求められ、確率変数を確率によって重み付けした場合の平均値を指します。確率変数の期待値はE(X)とあらわします。

確率分布の分散は、期待値を基準とした確率分布のばらつきのことであり、V(X)であらわします。分散が大きいほど実現値のバラつきが大きく、それぞれが起こる確率は低くなります。

代表的な確率分布

事象の性質によってさまざまな確率分布があり、その数は数十種類に及びます。そのなかから、二項分布を中心に関連のある確率分布をご紹介します。

二項分布 ［B（n,p）］

コイントスの表裏のような起こりうる事象が2つの場合に、独立な試行を複数回行った結果、一方の事象が起こる確率分布が二項分布です。

とり得る事象が2つである試行をベルヌーイ試行といい、ベルヌーイ試行は以下の条件を満たすものです。

• 試行の結果として起こる事象が2つのいずれかである
• 複数回行った場合の各試行は独立している（他の試行に影響しない）
• 一方の事象が起こる確率がp、もう一方の事象の起こる確率が（1ーp）で一定である

ベルヌーイ試行を1回だけしか行わない場合の二項分布をベルヌーイ分布といいます。

二項分布の確率質量関数は以下の式で表されます。 P(X＝k)＝nCk pk (1ーp)n-k n：試行回数    p：一方の事象が起こる確率   k：一方の事象が起こる回数 期待値 ：E(X) ＝ np 分散     ：V(X) ＝ np（1ーp） 離散型確率分布

二項分布は試行回数と一方の事象が起こる確率さえわかれば求めることができます。

マーケティングリサーチとは｜基礎から応用まで徹底解説

マーケティングリサーチの意味、目的、条件、方法、必要なことなどを詳細解説。マーケティングリサーチの必須情報が詰まっています。

QiQUMOコンテンツ

下のグラフは試行回数10回、確率が0.5の場合の二項分布を描いたものです。期待値は5で、分散は試行回数を増やしていくと、横に広がる山を描き、最大値は小さくなっていきます。

二項分布のグラフは以下のようになります。

・試行回数：10回

・一方の事象が起こる回数：1～10

・一方の事象が起こる確率：0.5

とした場合のグラフです。

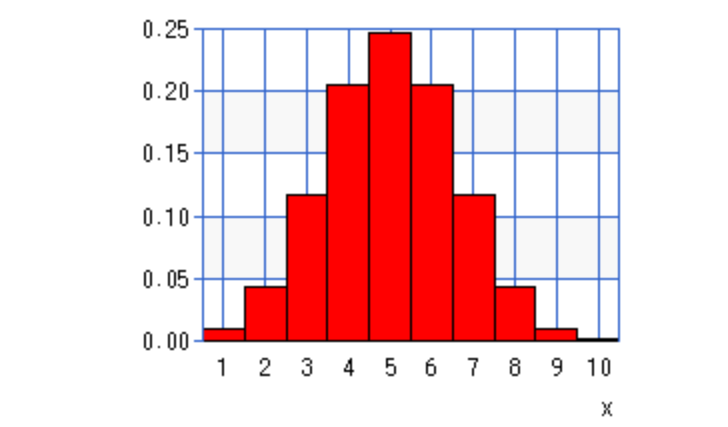
二項分布の例

• コイントスを行った場合の表、または、裏が出る確率分布
• 成功するか失敗するかの二択の確率分布 など

ポアソン分布［Po（λ）］

ポアソン分布は、単位時間や単位空間など一定の範囲において、稀にしか起こらない事象の確率分布のことです。稀にしか起こらない事象が起こるか起こらないかを対象とするため、ポアソン分布は二項分布に関連しています。

過去の結果をもとに平均すると λ（ラムダ）回起こるとわかっている場合（期待値がλである場合）、その場合の確率pは λ / nとなります。

p＝λ / nを二項分布の確率質量関数に代入すると以下の公式が得られます。（導出過程は省略します。）

ポアソン分布の確率質量関数は以下の式で表されます。 P(X＝k)＝e- λ λkk! λ：平均値（期待値）     k：稀な事象が起こる回数     e：ネイピア数（自然対数の底） 期待値 ：E(X) ＝ λ 分散     ：V(X) ＝ λ 離散型確率分布

二項分布において、np＝λ＞0を固定してnを大きくしていったものがポアソン分布です。ポアソン分布は、期待値と分散がλと等しくなることに特徴があります。

下のグラフの例は、1,000個の製品を生産する場合に、不良品の発生率が0.3%とした場合のポアソン分布を描いたものです。

np＝λ＞0より、n＝1,000個、p＝0.003なので、λ＝3を確率質量関数に代入すると以下のグラフが得られます。

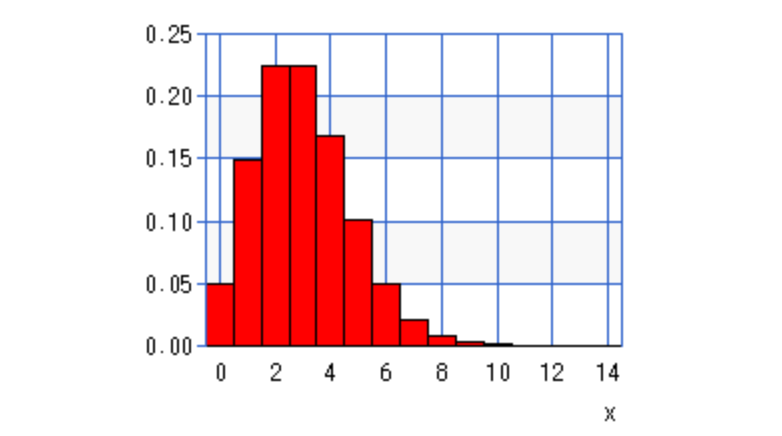
ポアソン分布の例

• 交通事故や自然災害の発生数
• コールセンターの入電数
• 製造業の不良品発生数 など

指数分布［Ex（λ）］

指数分布はランダムに起こる事象の時間間隔の確率を与える連続確率分布です。ポアソン分布が事象の発生回数（何回起こるか）の確率を求めるのに対し、指数分布は事象の発生間隔（次に起こるまでの時間）の確率を求めます。

事象が起きてから次の事象が起こるまでの間隔はランダムであり、それぞれの間隔は互いに影響することはありません。このことを無記憶性といいます。

以下のグラフを見て分かるとおり、指数分布の確率密度関数は単調減少する値をとり、x＝0のところでλ（平均の発生回数）の最大値となります。

確率密度が、x＝0で最大値をとりxの増加に従って単調減少するのは、次の事象が発生するx時間後までに事象が起こらない確率を積算する必要があるからです。

単位時間あたりの発生回数 λ と単位時間に対する求める間隔の比率 x がわかれば、以下の公式から xまでに次の事象が発生する確率密度を求めることができます。

指数分布の確率密度関数は以下の式で表されます。 f(x)＝λe- λx （x≧0） λ：単位時間当たりの平均発生回数      x：次の事象が起こるまでの時間     e：ネイピア数 期待値 ：E(X) ＝ 1λ 分散     ：V(X) ＝ 1λ2 連続型確率分布

下のグラフの例は、1時間あたりの平均来店客数を10人、5人、3人とした場合の10分ごとの確率密度の変化をあらわしたものです。

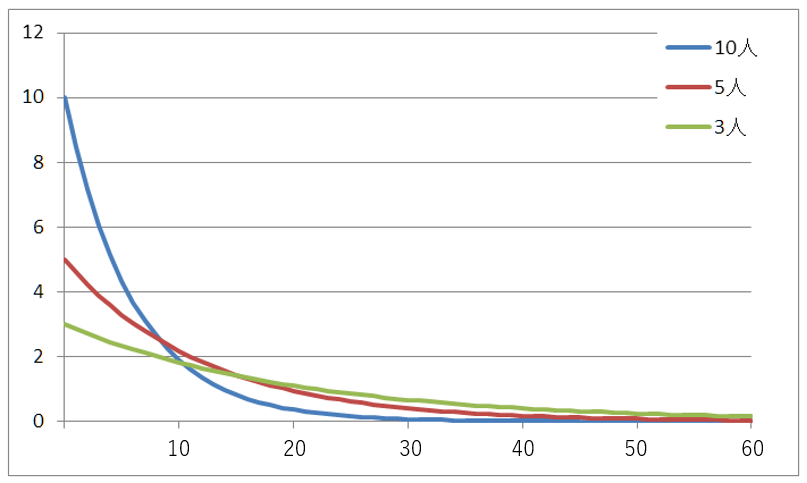
指数分布の例

• コールセンターの入電の間隔
• 地震の発生間隔
• 行列の待ち時間 など

ガンマ分布［Ga（a,b）］

ガンマ分布は一定の発生確率を持つ事象が、k回発生するまでの時間間隔の確率分布です。指数分布は次の事象が起こるまでの時間についての確率密度を求めますが、ガンマ分布は事象が複数回起こるまでの時間の確率密度を求めます。

ガンマ分布は指数分布を一般化させたものです。指数分布が単位時間当たりの発生回数という1つのパラメーターによって分布が決まるのに対し、ガンマ分布は事象が起こる回数（形状母数）と、事象が1回起こる平均的な時間（尺度母数）の2つのパラメーターに依存します。

ガンマ分布の確率密度関数は以下の式で表されます。 f(x)＝1Γ(k)θkxk-1e-xθまたは f(x)＝λkΓ(k)xk-1e-λx k：事象が起こる回数（尺度母数）θ：事象が1回起こる平均的な期間（形状母数）x：事象が起こるまでの期間（確率変数）λ：λ＝1θΓ：Γ(k)＝(kー1)! （k は正の整数）e：ネイピア数 期待値 ：E(X) ＝kθ＝ kλ 分散     ：V(X) ＝kθ2 ＝kλ2 連続型確率分布

下のグラフは、3年に1度故障する部品のガンマ分布を描いたものです。

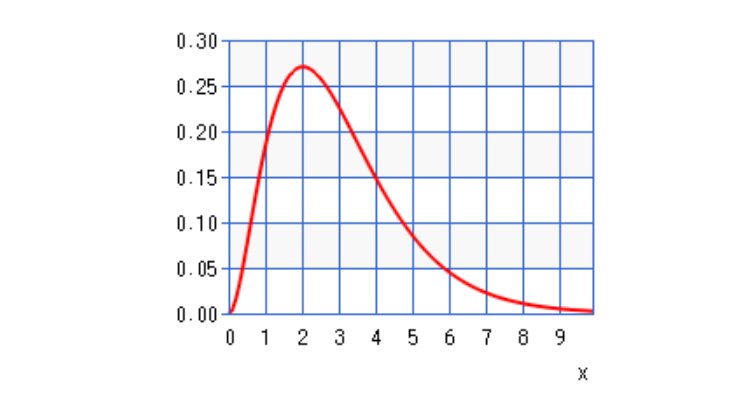
ガンマ分布の例

• ウイルスの潜伏期間
• 電子部品の寿命
• 保険金の支払額 など

正規分布とは｜簡単解説

正規分布とは 正規分布を理解していただくために、以下のグラフをご覧ください。左右対称の釣鐘型のグラフですが、これが正規分布を表しています。 ドイツの数学者であり…

QiQUMOコンテンツ

まとめ

確率分布は統計を使った推定や予測、検定をはじめとして、データのモデリングや不確実性の評価など、さまざまな場面で用いられます。確率分布には多くの種類があり、それぞれに数学の知識が求められますが、実務のなかで必要な分析に対応する確率分布をひとつひとつ覚えていくとよいでしょう。