カイ二乗検定とは|簡単解説

カイ二乗検定のカンタン解説
カイ二乗検定はカテゴリカル・データの変数について、観測された度数と期待される度数の差から検定統計量を求める仮説検定の手法です。アンケートのクロス集計表で表頭・表側の変数に関連があるかどうかを調べる際に用います。
カイ二乗検定とは
仮説検定の手法のひとつであるカイ二乗検定には以下の特徴があります。また、カイ二乗検定は「適合度の検定」「独立性の検定」「母分散の検定」に用いられます。
仮説検定の手続きを取る
カイ二乗検定は仮説検定の一手法であり、帰無仮説と対立仮説を設定し、設定した有意水準から求められるp値を求めます。検定統計量として求めるカイ二乗値(χ²)を比較することで、とり得る仮説を主張します。
カテゴリカルデータを対象とする
カイ二乗検定は、質的変数(カテゴリカル・データ)の度数を検定の対象とします。
カイ二乗分布による検定
カイ二乗分布は標準正規分布からランダムにデータ一定数取得して2乗和を計算した時に描かれる確率分布です。検定の対象となる変数から自由度を求め、自由度に応じた確率分布を基準として検定を行います。
適合度検定
適合度の検定は観測された度数分布が、期待される確率分布から計算される度数分布に当てはまるかどうかを確かめることです。
次のような例が適合度の検定に当てはまります。
【例】
サイコロの1〜6までの各目の出る確率は1/6ですが、実際にサイコロを60回振って、1〜6までのそれぞれの目が出た回数が以下のように観測されたとします。
| サイコロの目 | 1 | 2 | 3 | 4 | 5 | 6 | 合計 |
| 各出た目の回数 | 9 | 9 | 13 | 11 | 10 | 8 | 60 |
各目の出る確率が1/6となるようにサイコロが正確に作られていると考えていいかどうかを、理論的な確率分布をもとに判定するのが適合度検定に当たります。
適合度検定は以下の手順で行います。
①帰無仮説と対立仮説を設定する
この場合の帰無仮説と対立仮説は次のようになります。
帰無仮説:
得られた観測結果は偶然(想定される確率分布に従う)対立仮説:得られた観測結果は偶然ではない(想定される確率分布とは異なる)
②期待度数を求める
正確に作られたサイコロの各目の出る確率は1/6です。これを理論的な確率とすると、60回試行した場合の各目の出る回数は10回づつであると考えられます。理論的な確率から計算される試行の結果が期待度数です。
適合度検定は観測度数と期待度数の差が確率分布の範囲内で偶然生じたものか、理論的な確率が当てはまらない何らかの理由があるのかを確かめるということです。
| サイコロの目 | 1 | 2 | 3 | 4 | 5 | 6 | 合計 |
|---|---|---|---|---|---|---|---|
| 観測度数(fi) | 9 | 9 | 13 | 11 | 10 | 8 | 60 |
| 理論的な確率(pi) | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1 |
| 期待度数(npi) | 10 | 10 | 10 | 10 | 10 | 10 | 60 |
③カイ二乗値(検定統計量)を求める
カイ二乗値(χ²)は観測度数と期待度数の差の2乗を期待度数で割ったものを合計して求めます。
サイコロの例でカイ二乗値(χ²)を計算すると以下のようになります。
χ²= (9-10)²10+(9-10)²10+(13-10)²10+(11-10)²10+(10-10)²10+(8-10)²10=1.1
この場合の自由度は、サイコロの目の数(カテゴリーの数)kから1を引いたものであり、自由度= 6 ー 1=5となります。
²(カイ二乗値) =i=1k(fi-npi)²npi 自由度=kー1
④カイ二乗分布表から棄却域を決める
カイ二乗分布表を参照し、有意水準(例:0.05)と自由度(k-1)に基づいて棄却域の下限となるカイ二乗値を確認します。
【カイ二乗分布表】
| 自由度 v | α = 0.99 | 0.975 | 0.95 | 0.90 | 0.10 | 0.05 | 0.025 | 0.01 |
| 1 | 0.00016 | 0.00098 | 0.0039 | 0.016 | 2.71 | 3.84 | 5.02 | 6.63 |
| 2 | 0.02 | 0.051 | 0.10 | 0.21 | 4.61 | 5.99 | 7.38 | 9.21 |
| 3 | 0.11 | 0.22 | 0.35 | 0.58 | 6.25 | 7.81 | 9.35 | 11.34 |
| 4 | 0.30 | 0.48 | 0.71 | 1.06 | 7.78 | 9.49 | 11.14 | 13.28 |
| 5 | 0.55 | 0.83 | 1.15 | 1.61 | 9.24 | 11.07 | 12.83 | 15.09 |
たとえば、有意水準を0.05に設定し、自由度が5の場合、棄却域の下限となるカイ二乗値は11.07です。
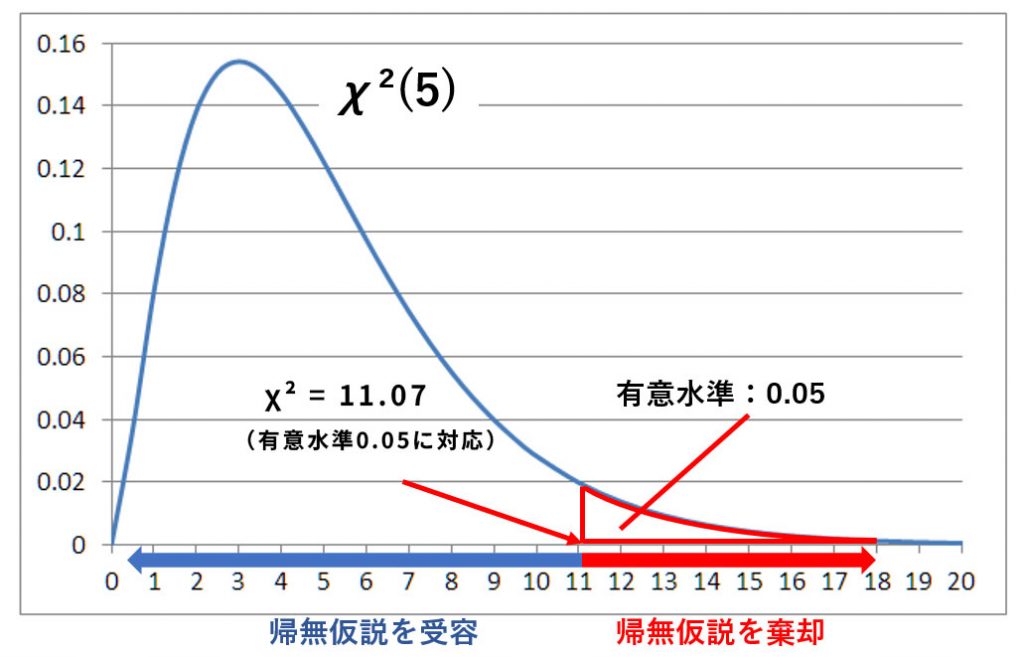
自由度5のカイ二乗分布において、カイ二乗値が11.07を超える確率は5%しかなく、これは有意水準0.05に対応する棄却域の境界値です。
観測値とカイ二乗検定の判断
今回、観測度数と理論的な確率から求めたカイ二乗値(χ²)は 1.1 でした。このときの p値は約0.088(正確には ≒ 0.0885) となります。
これは p値 = 0.088 > 有意水準 = 0.05 であるため、帰無仮説「得られた観測結果は偶然(理論分布に従う)」は棄却されず、このデータからはサイコロが不正に偏っているとは言えず、サイコロは正確に作られていると結論づけることができます。
独立性の検定
独立性の検定は、2つの変数が独立(関連がない)かどうかを統計的に調べる方法です。クロス集計表(分割表)で表されるデータに対し、関連がなければ独立、関連があれば独立ではないと結論づけます(関連があっても因果まで直ちには断定できません)。
次のような例が独立性の検定に当てはまります。
【例】ワクチンの効果を調べるため、予防接種の有無とインフルエンザ罹患の2変数について600人を調査したところ、次の結果が得られました。
| インフル罹患 | インフル感染せず | 合計 | |
|---|---|---|---|
| 予防接種あり | 70 | 80 | 150 |
| 予防接種なし | 330 | 120 | 450 |
| 合計 | 400 | 200 | 600 |
このとき、予防接種の有無と罹患の独立性を検定します。独立性の検定は以下の手順で行います。
①帰無仮説と対立仮説を設定する
この場合の帰無仮説と対立仮説は次のようになります。
帰無仮説 H_0:2変数は独立(予防接種と罹患は関連がない)
対立仮説 H_1:2変数は独立ではない(関連がある)
②期待度数の計算(H_0が成り立つ前提)
帰無仮説のもとで期待される値(期待度数)は次のように計算します
接種なし・非罹患:450 × 200 ÷ 600 = 150。
接種あり・罹患:150 × 400 ÷ 600 = 100
接種あり・非罹患:150 × 200 ÷ 600 = 50
接種なし・罹患:450 × 400 ÷ 600 = 300
| 罹患(期待) | 非罹患(期待) | 合計 | |
|---|---|---|---|
| 予防接種あり | 100 | 50 | 150 |
| 予防接種なし | 300 | 150 | 450 |
| 合計 | 400 | 200 | 600 |
③カイ二乗統計量の計算
カイ二乗値(χ²)は、次の式で計算されます。
χ² = (70-100)²/100 + (80-50)²/50 + (330-300)²/300 + (120-150)²/150
= 900/100 + 900/50 + 900/300 + 900/150
= 9 + 18 + 3 + 6
= 36
自由度は (行数−1) × (列数−1) = (2−1)(2−1) = 1
④棄却域と判断
有意水準を 5%(α=0.05)とした場合、自由度1のカイ二乗分布表における臨界値(χ²の閾値)は 3.84 です。これは χ² が 3.84 以上なら帰無仮説を棄却する、という意味です。
注:3.84 は p値ではありません。p値は 観測された χ² から上側確率を計算して求めます(例:本例の χ²=36 なら p ≈ 1.97×10⁻⁹ < 0.05 なので棄却)。
臨界値(χ²の境界値) = 3.84(自由度1, α=0.05)
この検定結果により、「予防接種の有無」と「インフル罹患」には統計的に有意な関連がある(独立ではない)と判断されます。
注:本検定は「関連の有無」を評価するものであり、「因果関係(=ワクチンが原因で罹患が減った)」まで証明するものではありません。
まとめ
カイ二乗検定はマーケティング分野以外にも、医療機関や製造業をはじめとしてさまざまな分野で用いられる仮説検定の手法です。
カイ二乗分布のp値はエクセルの関数CHISQ.DISTで求めることができるため、実務にも取り入れやすい検定手法であるといえます。






