ベイズの定理とは|簡単解説

ベイズの定理のカンタン解説
ベイズの定理は確率と不確実性を扱うベイズ統計学の基盤となる公式です。観測されたデータと曖昧な情報を含む事前確率から事後確率を求めるという点で従来の統計学とは異なる考え方とされています。ベイズ統計学の基本となる確率の公式がベイズの定理です。
ベイズの定理とは
ベイズの定理とは以下の公式のことです。
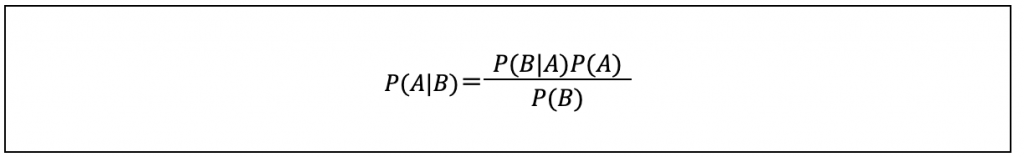
【ベイズの定理公式】
PA|B=P(B|A)P(A)P(B)
ベイズの定理は条件付き確率から導きだすことができます。事象Aと事象Bが同時に起こる確率を積事象といいます。
事象Aと事象Bが独立である場合、P(A∩B) =P(A)P(B)とあらわされます。
条件付き確率は、事象Aが起こったときに事象Bが起こる確率、または、事象Bが起こったときに事象Aが起こる確率なので、以下の式であらわされます。

① 事象Aが起こったときに、事象Bが起こる確率 :P(B|A) = P(A∩B)P(A)
② 事象Bが起こったときに、事象Aが起こる確率:P(A|B) = P(A∩B)P(B)
①を移項して P(A∩B)=P(B|A)P(A) 、②に代入するとベイズの公式が導かれます。
P(A|B) = P(B|A)P(A)P(B)
ベイズの定理ではPA|Bを事後確率、PB|Aを尤度、PAを事前確率と呼びます。
事後確率=PA/B:事象Bが起こった時に、事象Aが起こる確率
事前確率=PA:事象Aが起こる確率
尤度=PB/A:事象Aが起こる確率
事象Aを原因、事象Bを結果としてベイズの公式を表してみます。

P(結果|原因)P(原因)
P原因|結果=ーーーーーーーーー
P(結果)
事後確率は結果を条件とした時の確率ということになります。尤度も条件付き確率で表されますが、ベイズの公式のなかでは原因となる事象が起こる確率の大きさという意味を持っています。
例えば、表と裏の出る確率がそれぞれ1/2のコインを10回投げたときに6回表が出る確率(0.2051)を求めるのが事後確率であるのに対し、コインを10回投げて6回表が出る確率が0.2051だったときに、コインを1回投げたときの表が出る確率を求めているのが尤度というのがざっくりとしたイメージです。
ベイズの定理の具体例
ベイズの定理を使った具体的な例をいくつかご紹介します。
不良品の確率
ある製造ラインの不良品の発生原因が、①ヒューマンエラーである確率が50%、②材料の不良である確率が20%、③機械の不良である確率が30%であり、それぞれの瑕疵による製品不良になる確率がわかっていたとします。
製品不良が1個発見された時に、それが材料不良が原因である確率をベイズの定理から求めてみます。
不良発生原因となる事象を A、 B、 Cとすると、それぞれの発生確率とその時の不良品の発生確率は以下のようになります。
| 不良の発生原因 | 瑕疵の発生確率 | 製品不良の発生確率 P(E) |
|---|---|---|
| ①ヒューマンエラー (A) | 50% P(A) | 0.2% P(E|A) |
| ②材料の不良 (B) | 20% P(B) | 0.1% P(E|B) |
| ③機械の不良 (C) | 30% P(C) | 0.3% P(E|C) |
すべての製品不良の発生確率 P(E) は以下の式で求められます。
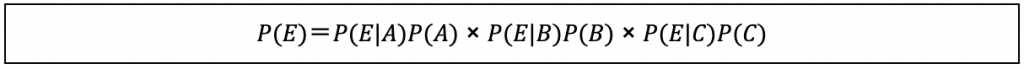
P(E)=P(E|A)P(A) × P(E|B)P(B) × P(E|C)P(C)
材料が不良である確率は20% P(B)、材料が不良である時に製品不良が発生する確率は0.1% P(E|B)です。
求めるのは、材料不良が原因となる場合の製品不良の確率なので、
P(B)P(E)=P(B|E)とあらわすことができます。求めるP(B|E)は以下のようになります。

P(B|E)=P(E|B)P(B)P(E) = P(E|B)P(B)P(E)=P(E|A)P(A) × P(E|B)P(B) × P(E|C)P(C)
=0.001 ×0.20.002 × 0.5 +0.001 ×0.2 + 0.003 × 0.3=0.0021=0.21%
モンティ・ホール問題
ベイズの定理でよく使われる事例としてモンティ・ホール問題があります。
アメリカのテレビ番組で行われたゲームの勝率に関する確率論が雑誌に投稿され、直感に反するものとして大きな議論を巻き起こしたというものです。
提起された問題は以下のようなゲームを想定しています。
①3つのうち1つに景品の用意されたドアがあり、プレーヤーが最初に1つのドアを選ぶ。
②当たりのドアを知っている司会者が、選ばれなかった2つのドアのうちハズレのドアを開ける。
③プレーヤーは最初に選んだドアから残ったドアに変更するかどうかを選択する。
3つのドアのうち、司会者がドアを開けることで1つのハズレのドアが確定し、残った2枚のドアのどちらかの景品が当たる確率は1/2なので、③でドアを変更してもしなくても当たる確率は変わらないというのが直感的な結論です。
しかし、ベイズの定理を使って考えると、③でドアを変えた場合に景品が当たる確率が2/3になることがわかります。
プレーヤーが最初に選ぶドアがA、司会者の開けるドアがBであるという前提を置いて、ベイズの定理に当てはめてみると次のようになります。
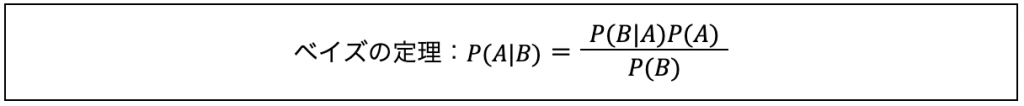
ベイズの定理:P(A|B) = P(B|A)P(A)P(B)
【ドアを変えないで当たるケース】
Aが当たりである確率:P(A)=1/3
プレーヤーがAを選んだ時に司会者がBを開ける確率:P(B)=1/2
Aが当たりのときに司会者がBを開ける確率:P(B|A)=1/2
(司会者はAが当たりであることを知っているので選べるのはBとC)
事後確率となるP(A|B)を求めると、

P(B|A)P(A) 1/2×1/3
P(A|B) = ーーーーーー =ーーーーーー =1/3
P(B) 1/3
【ドアを変えて当たるケース】
Cが当たりである確率:P(C)=1/3
プレーヤーがAを選んだ時に司会者がBを開ける確率:P(B)=1/2
Cが当たりの時に司会者がBを開ける確率:P(B|C)=1
(司会者はCが当たりであることを知っているので選べるのはBのみ)
この場合の事後確率P(C|B)は、
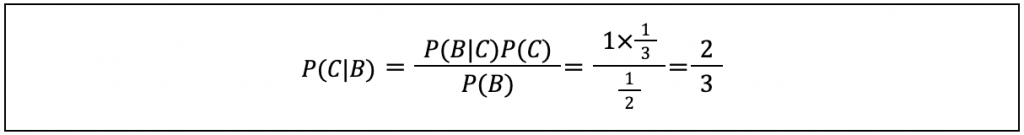
P(B|C)P(C) 1×1/3
P(C|B) =ーーーーーーー=ーーーーー=2/3
1/2
この結果からドアを変えたほうが当たる確率が高くなることがわかります。
ベイズの定理を使わずに確率の問題として考える場合、プレーヤーが最初に選んだドアと,
司会者が1つ開けた後に選ぶドアの組み合わせのうち、当たりの事象から確率を求めます。
| プレーヤーの選択 | A | B | C | ||||||
| 当たりのドア | A | B | C | A | B | C | A | B | C |
| 変更しない場合に当たる | ◯ | ◯ | ◯ | ||||||
| 変更した場合に当たる | ◯ | ◯ | ◯ | ◯ | ◯ | ◯ | |||
プレーヤーが選ぶドアの組み合わせが9通りあり、ドアを変えなかった場合の当たりの組み合わせが3通り、変えた場合の当たりの組み合わせが6通りなので、変えたほうが当たる確率が高いということです。
まとめ
ベイズの定理を基盤とするベイズ統計学に対して、従来の統計学は頻度主義的統計学と区別されます。ベイズ統計学は不確実性を受け入れるという点が頻度主義的な統計学とは大きく異なる点であり、コンピュータの計算能力の向上とともに活用の幅が広がってきている分野でもあります。
統計学全般の知識がないと理解が進まないところがありますが、まずはベイズの定理を理解するところから始めてみましょう。



