最小二乗法とは｜簡単解説
アドミンアドミン
最小二乗法のカンタン語句解説
最小二乗法は取得したデータに関数を近似（フィット）させる方法のひとつで、関数により与えられる予測値と取得データの残差平方和を最小とする係数と切片を求めます。最小二乗法は回帰分析を行う際の手法であるほか、分散分析や因子分析にも使われます。
最小二乗法とは
最小二乗法を「取得したデータを関数を用いて近似させる方法」と述べましたが、データの関係性を関数であらわすことができれば、データの誤差を除いたりデータから予測したりすることができます。
例えば、以下の左のグラフのようなデータがある場合、xの増加に従いyも増加する１次関数で表されるx、yの関係性が推測できます。
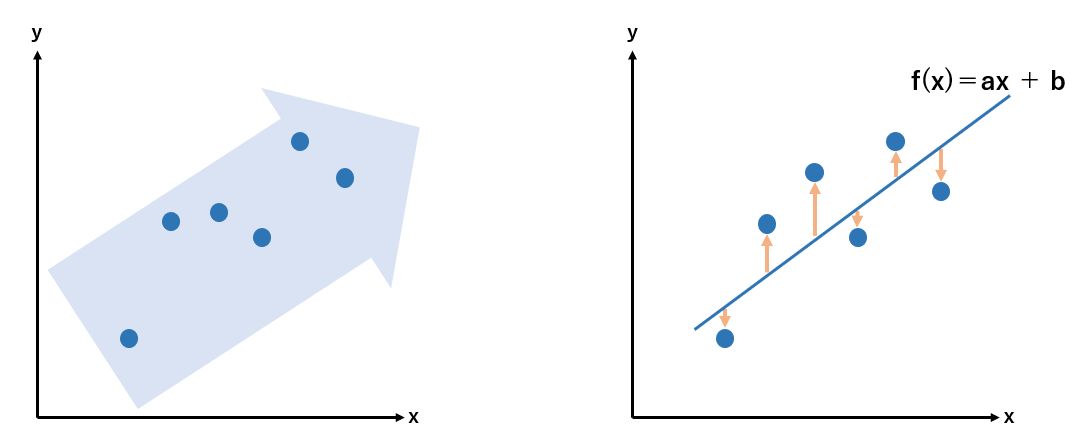
これを、右側のグラフの矢印（残差※）の長さの2乗和が最小になる関数 f(x)を求めるのが最小二乗法です。
この場合の f(x)＝ax＋bが回帰直線であり、係数aと切片bを求めればデータに近似する直線を描くことができます。
※残差：観測値と 推定するモデルである f(x)との差。誤差は観測された値であり計算では求められないが、残差は計算で求めることができる。偏差は観測値と平均値との差。
最小二乗法による f(x) の求め方
最小二乗法で求める回帰式は1次関数に限りませんが、ここでは直線で表されるf(x)＝ax+bを回帰式として説明します。
データを（x1,y1）,（x2,y2）,・・・（xi,yi）とすると、データの残差は yiー(axi＋b)です。
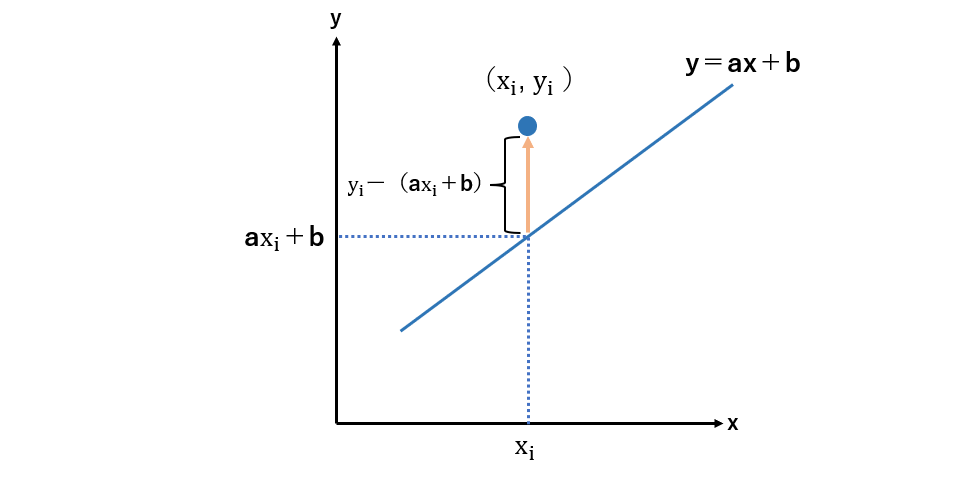
データ個数分の残差を2乗したものの合計は以下の式であらわされます。
{y1ー(ax1＋b)}2＋{y2ー(ax2＋b)}2＋・・・{yiー(axi＋b)}2＝i=1n{yiー(axi＋b)}2
係数aと切片bは以下の式で求められます。
a＝SxySx2 b＝yーax
Sxy：xとyの共分散 Sx2：xの分散 x,y：変数の平均値
ここから具体的なデータを使って回帰式を求めてみます。
x,yのデータは以下のものとし、xの分散とx,yの共分散を求めます。
| x | y | x偏差 | y偏差 | x偏差2 | x偏差×y偏差 |
|---|---|---|---|---|---|
| 10 | 40 | -25 | -45 | 625 | 1125 |
| 20 | 60 | -15 | -25 | 225 | 375 |
| 30 | 60 | -5 | -25 | 25 | 125 |
| 40 | 100 | 5 | 15 | 25 | 75 |
| 50 | 130 | 15 | 45 | 225 | 675 |
| 60 | 120 | 25 | 35 | 625 | 875 |
| x平均35 | y平均85 | ー | ー | xの分散291.7 | x,yの共分散541.7 |
ｘ,yの偏差を求め、x偏差2の平均であるxの分散とx偏差とy偏差の積の平均であるx,yの共分散を求めます。
f(x)＝ax+bの係数aは a＝SxySx2 であることから、a＝541.7 / 291.7 ＝1.857
切片bは b＝yーax であることからb＝85ー1.857×35＝20.005
となり、回帰式は y＝1.857x＋20.005と求められます。
分散とは｜簡単解説 - QiQUMOコンテンツ
分散とは 基本統計量は平均や中央値などのデータ全体を一つの値に要約するための代表値と、データ全体のバラつき具合を表す散布度に分けられます。分散は散布度を表す基本…
QiQUMOコンテンツ 
回帰係数を求めるエクセルの関数
上記で計算したy-ax+bの係数aと切片bはエクセルのLINEST関数を使って求めることができます。
LINEST関数で書式は以下のようになります。
＝LINEST（yの範囲,xの範囲,定数,補正）
引数はyの範囲から入力することに注意が必要です。
定数と補正はTRUEまたはFALSEを指定し、以下の内容が適用されます。
| TRUE | FALSE | |
|---|---|---|
| 定数 | y=ax+bのaとbを出力。省略した場合はTRUEが指定される。 | y＝ax+bの定数bを0として係数aのみが出力される。 |
| 補正 | 標準誤差、決定係数、F補正項などの追加情報が出力される。 | 上記係数と定数のみ出力。省略可。 |
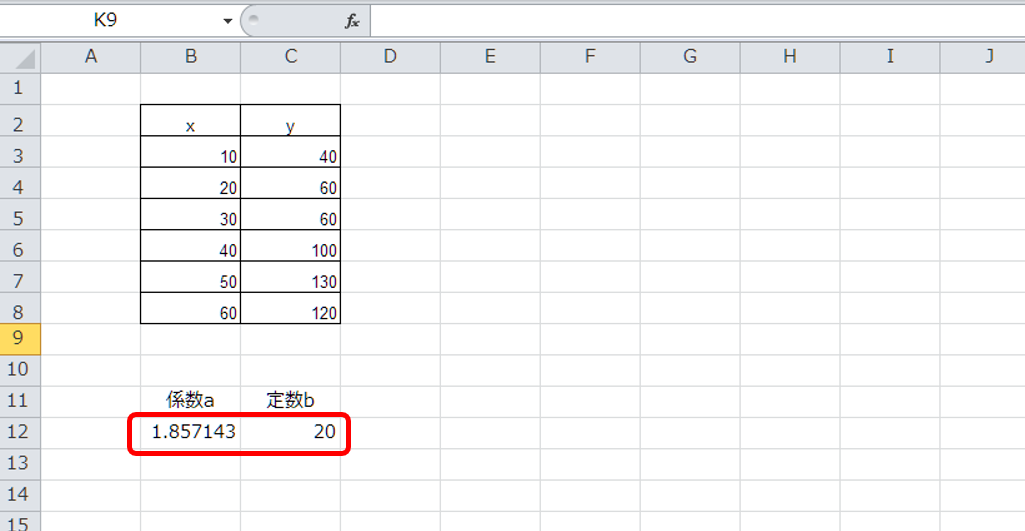
y=ax+bの係数aと定数bが出力されるため、あらかじめ出力される2つのセルを指定しておきます。
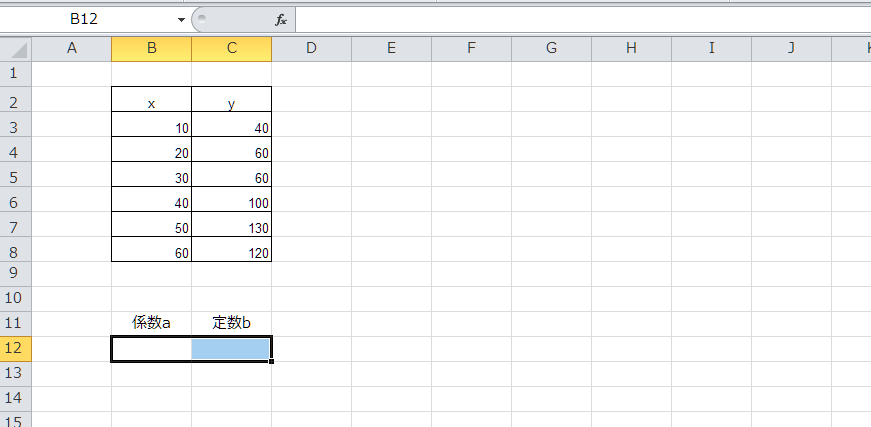
関数LINESTを選び、yの範囲とxの範囲のセルを指定します。定数と補正は省略することが可能です。
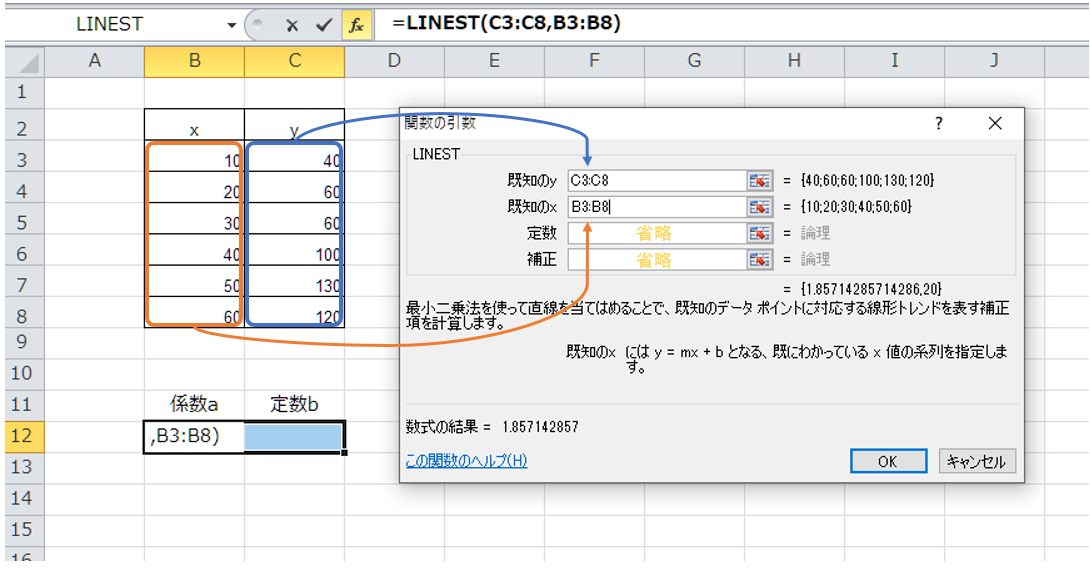
上記の状態から「Ctrl」＋「Shift」＋「Enter」を押すと、最初に範囲指定した2つのセルに係数aと定数bの値が出力されます。
エクセルの近似曲線オプションで回帰直線を描く
エクセルで散布図を作成すると、プロットされた点に近似した曲線を自動的に描いてくれる機能があります。
まず、データから散布図を作成します。
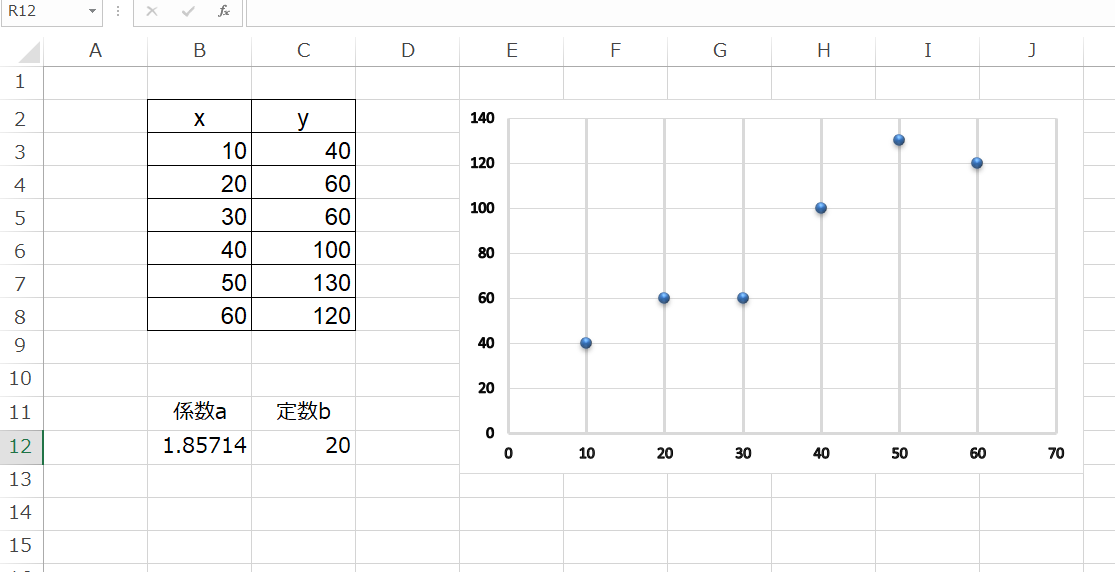
グラフを選択すると「グラフツール」が表示されるので、「グラフ要素を追加」から「近似曲線」、「その他の近似曲線オプション」を選びます。
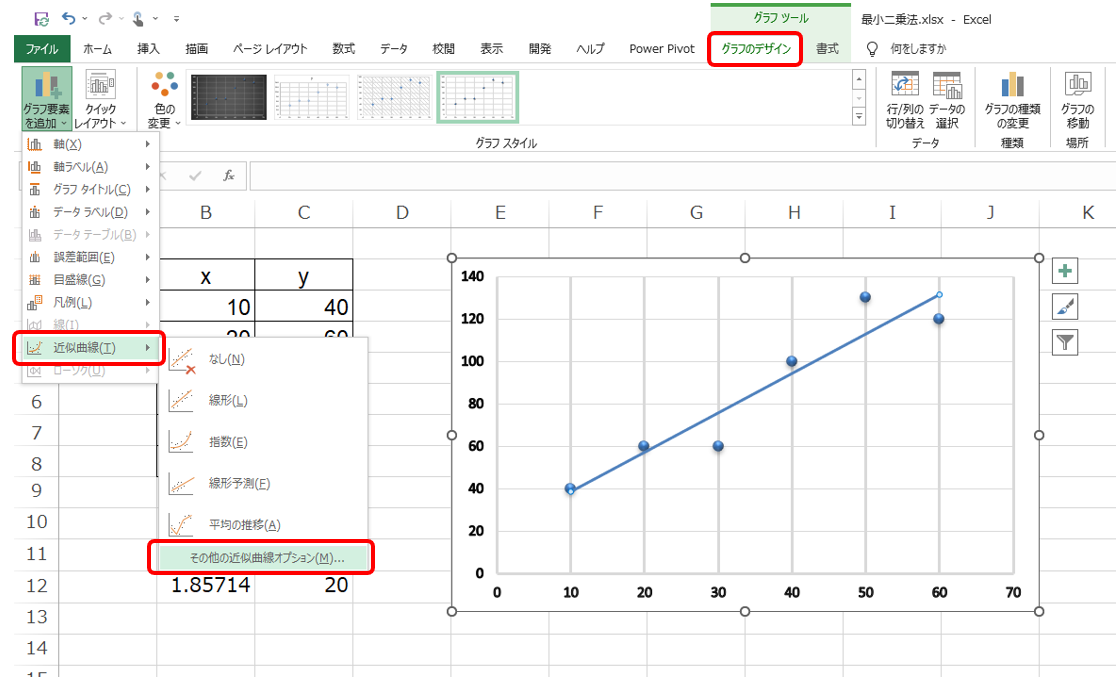
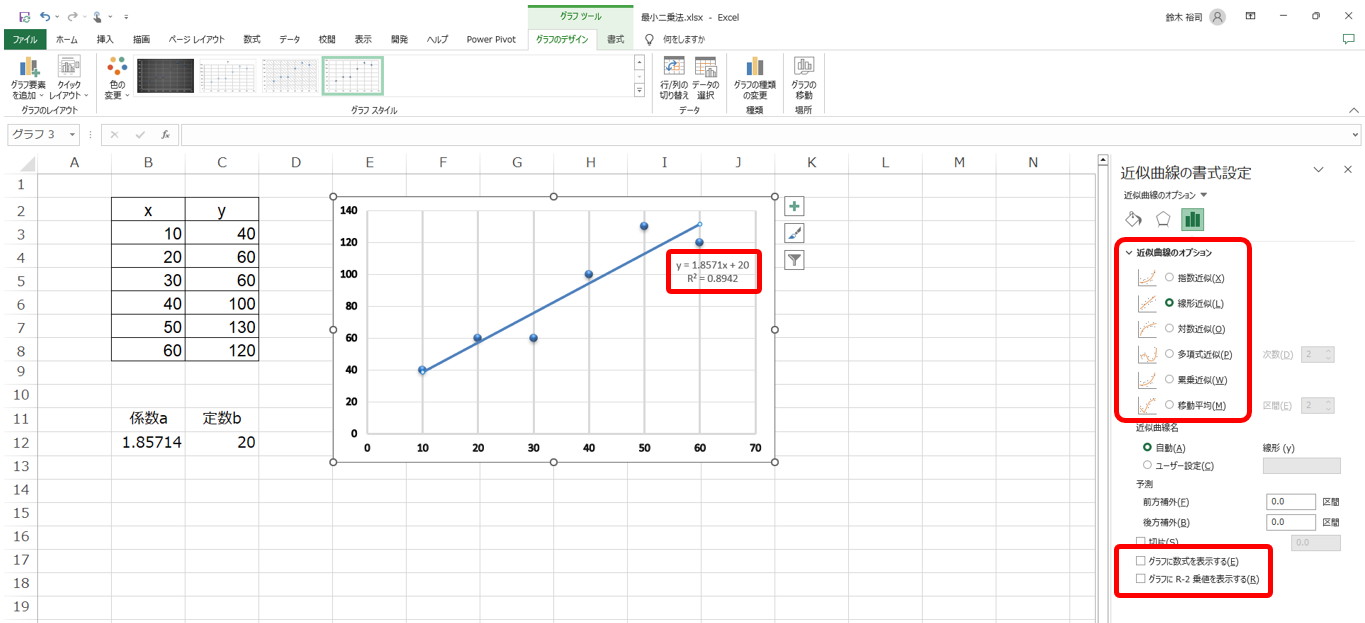
「近似曲線（T）」からそのまま「線形（L）」を選択すると回帰直線が描かれます。「その他の近似曲線オプション（M）」から「グラフに数式を表示する（E）」「グラフにR2乗値を表示する（R）」を選択すると回帰式と決定係数R2を表示させることができます。
決定係数について
決定係数R2とは、求めた回帰直線がデータに対してどの程度当てはまっているかどうかを判断する指標です。
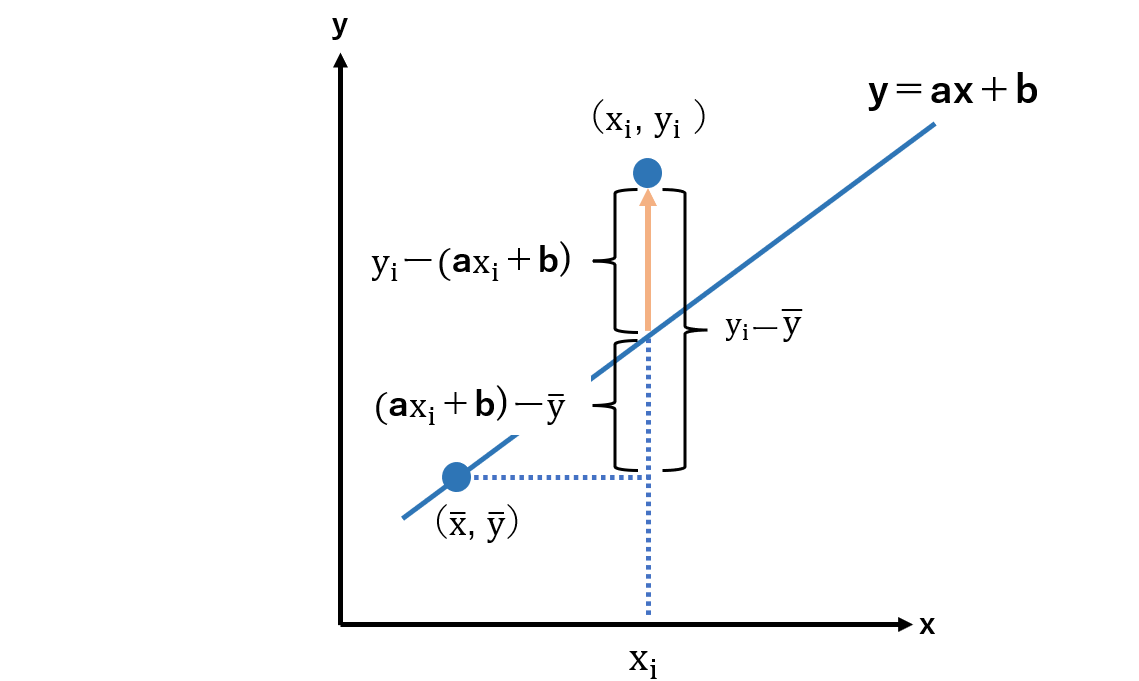
b＝yーax からy＝ax+bは（x,y）を通ることがわかっています。(xi,yi)における偏差 yiーyの大きさのうち、残差 yiー(axi+b)の割合が小さいほど回帰直線の当てはまり具合が良いということになります。
データ全体について求めるために以下の式を用います。
R2（決定係数）＝i-1n{(axi＋b)ーy}2i-1n(yiーy)2
決定係数R2は割合であるため、0≦R2≦1の値を取り、1に近いほど回帰直線の当てはまりが良いということになります。
前述のエクセルの近似曲線オプションで求めたR2は0.8942であり、目的変数の約9割を回帰直線によって説明できることを表しています。
まとめ
最小二乗法はエクセルを使うことによって簡単に結果を求めることができますが、線形回帰分析のなかでの最小二乗法の使い方を知っておくことは、他の高度な分析手法を学ぶ上での基本となります。
また、最小二乗法は回帰分析以外にも画像処理のノイズ除去や誤差を最小化するためのモデルを求める際など幅広く用いられるため、考え方のイメージをつかんでおくことが役に立ちます。
